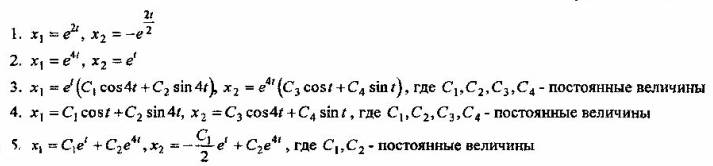Тесты
Сборник заданий
Дата сдачи: Июль 2008
Задание 1
Изучить п. 1.1. раздела 1. Изучить и законспектировать п. 1.2. раздела 1. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Когда возникла идея о бесконечности числового ряда?
1. В I веке до н.э.
2. Во II веке до н.э.
3. В III веке до н.э.
4. В IV веке до н.э.
5. В V веке до н.э.
Вопрос 2. Какое из чисел не является рациональным?
1. ½
2. 0.1
3. 0.111…
4. π = 3.14…
5. 1/7 = 0.142857142857…
Вопрос 3. Какое из чисел не является действительным?
1. е (основание "натуральных логарифмов")
2. π = 3.14...
3.1/7
4. ![]()
5. ![]()
Вопрос 4. В какой строке свойство кватернионов записано с ошибкой?
1. i2 = -1
2. i2 = j2
3. k2 = -1
4. jk = i
5. kj = jk
Вопрос 5. Какое трансфинитное число получится в результате увеличения трансфинитного числа х0 на 1000000?
1. х0
2. х1
3. х2
4. 1000000
5. х2 - 1000000
Задание 2
Изучить и законспектировать п. 1.3. раздела 1.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Как можно сформулировать основные направления математических исследований в общественных науках?
1. Исследования в области линейного программирования
2. Исследования в области нелинейного программирования
3. Исследования в области экономики
4. Исследования в области кибернетики
5. Исследования в части точного описания функционирования общественных систем и их частей и исследования влияния сознательного воздействия (управления) на функционирование социальных структур и течение социальных процессов.
Вопрос 2. Какое предположение лежит в основе использования матрицы коэффициентов выживаемости и рождаемости?
1. Предположение о неизменности выживаемости и рождаемости
2. Предположение об однородной возрастной структуре
3. Предположение о прекращении эпидемий на рассматриваемом временном интервале
4. Предположение об отсутствии войн
5. Предположение об отсутствии стихийных бедствий
Вопрос 3. Какая гипотеза является следствием рассмотрения модели изменения численности аристократов в племени Нетчез?
1. Количество аристократов в племени было стабильным
2. Племя не имело стабильной классовой структуры
3. Племя вело жестокие войны
4. Количество «парий» (неимущих) в племени постоянно возрастало
5. Общая численность племени не могла быть стабильной
Вопрос 4. Какая из гипотез не использовалась в простейшей модели экономического роста?
1. Общий доход равен сумме затрат на предметы потребления и сбережений
2. Сбережения равны затратам на средства труда
3. Доля сбережений не равна нулю
4. Производство дополнительной продукции пропорционально дополнительным капиталовложениям
5. Poст производства дополнительной продукции опережает рост затрат
Вопрос 5. Как чаще всего целесообразно решать проблему, возникающую при необходимости учета дополнительных факторов в очень большой и сложной экономической модели?
1. Ввести в модель новые категории и зависимости
2. Постараться выделить (разработать) подмодели, в которых будут учтены дополнительные факторы
3. Разработать модель заново с учетом дополнительных факторов
4. Упростить модель, затем учесть дополнительные факторы
5. Учесть в модели всю имеющуюся информацию
Задание 3
Изучить материалы части 1 части 2. Выписать определения, постулаты и аксиомы Евклида. Выписать определение обоснования геометрия. Из школьного учебника по геометрии или из справочника по математике выписать формулировки признаков равенства и подобия треугольников, признаки параллельности прямых, теорем о сумме углов треугольника и многоугольника, основные формулы площадей геометрических фигур. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какая из геометрических фигур не изучается планеметрией?
1. Треугольник
2. Ромб
3. Параллелепипед
4. Окружность
5. Параллелограмм
Вопрос 2. Какая из формулировок является определением?
1. Существуют по крайней мере две точки
2. Каждый отрезок можно продолжить за каждый из его концов
3. Два отрезка, равные одному и тому же отрезку, равны
4. Прямой АВ называется фигура, являющаяся объединением всевозможных отрезков, содержащих точки А и В
5. Каждая прямая разбивает плоскость на две полуплоскости
Вопрос 3. Какая из формулировок о параллельных прямых но смыслу совпадает с пятым постулатом Евклидовских "Начал"?
1. Через точку, не лежащую на данной прямой, проходит единственная прямая, не пересекающая данную прямую
2. Две параллельные прямые при пересечении их третьей прямой образуют равные соответственные и внутренние накрест лежащие углы
3. Если прямая пересекает две другие прямые так, что внутренние односторонние углы с каждой из них оказываются в сумме меньше 180°, то эти прямые пересекаются по ту сторону от прямой, по какую лежат эти углы
4. Две прямые, перпендикулярные третьей прямой, параллельны
5. При пересечении двух параллельных прямых третьей сумма внутренних односторонних углов равна 180°
Вопрос 4. Найдите ложное утверждение.
Два треугольника равны, если они имеют соответственно равные:
1. три стороны
2. три угла
3. сторону и два прилежащих угла
4. два катета
5. гипотенузу и катет
Вопрос 5. Найти пару равновеликих геометрических фигур.
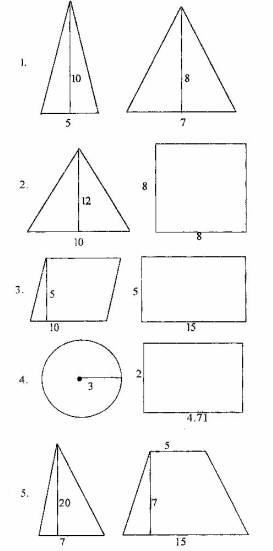
Задание 4
Изучить материалы п.п. 2.1, 2.2 части 2 части 2. Выписать утверждения, равносильные V постулату Евклида. Выписать аксиому параллельности Лобачевского и простейшие свойства плоскости Лобачевского, непосредственно вытекающие из аксиом.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое утверждение противоречат V постулату Евклида?
1. Множество точек, лежащих по одну сторону от данной прямой на одном и том же расстоянии от нее, есть прямая
2. Сумма углов треугольника равна 180°
3. Существуют подобные неравные треугольники
4. Сумма углов всякого четырехугольника меньше 360°
5. Две параллельные прямые при пересечении их третьей прямой образуют равные соответственные углы
Вопрос 2. Какое из высказываний является аксиомой параллельности Лобачевского?
1. Через точку, не лежащую на данной прямой, проходит единственная прямая, не пересекающая данную прямую
2. Две прямые, параллельные третьей прямой, параллельны между собой
3. Существует такая прямая а и такая, не лежащая на ней точка А, что через точку А проходит не меньше двух прямых, не пересекающих прямую а
4. Две прямые, перпендикулярные третьей прямой параллельны
5. Прямые, не имеющие общих точек, называются параллельными
Вопрос 3. По равенству каких из заданных соответствующих элементов двух треугольников в геометрии Евклида делается вывод о подобии треугольников, а в геометрии Лобачевского - вывод о равенстве треугольников?
1. По трем сторонам
2. По двум сторонам и углу между ними
3. По катету и гипотенузе
4. По стороне и двум прилежащим углам
5. По трем углам
Вопрос 4. Указать число, которое не может быть суммой углов четырехугольника на плоскости Лобачевского:
1. 100°
2. 270°
3. 300°
4. 330°
5. 360°
Вопрос 5. Указать число, которое не может быть суммой углов сферического треугольника:
1. 440°
2. 190°
3. 170°
4.360°
5. 510°
Задание 5
Изучить материалы п.п. 3.1 - 3.5. части 3 части 2, особое внимание уделить понятиям непротиворечивости и минимальности системы аксиом. Выписать формулировку сущности аксиоматического метода, перечисление основных понятий планиметрии, перечень групп аксиом и аксиомы I группы. Законспектировать основные этапы построения модели Пуанкаре планиметрии Лобачевского и арифметической модели системы аксиом евклидовой планиметрии в части аксиом I и V групп.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из понятий не является основным и подлежит определению в планиметриях Евклида и Лобачевского?
1. Отношение "точка В лежит между точками А и С"
2. Точка
3. Расстояние
4.Угол
5. Прямая
Вопрос 2. Найдите аксиому I группы.
1. Для любой прямой существуют ровно две полуплоскости, ограниченные этой прямой
2. Существуют по крайней мере три точки, не лежащие на одной прямой
3. Для любых точек А и В выполняется равенство |АВ| = |ВА|
4. Равенство |АВ| + |BС| = .АС| выполняется тогда и только тогда, когда точка В принадлежит отрезку АС
5. Всякое движение есть взаимно однозначное соответствие
Вопрос 3. Какое из высказываний непосредственно следует из аксиом принадлежности?
1. Пусть прямая а не проходит через точки А, В и С. Тогда если прямая а пересекает отрезок АВ, то она пересекает еще один и только один из отрезков ВС или АС
2. Если луч с началом в вершине угла проходит через внутреннюю точку угла, то все его точки, кроме начала, лежат внутри угла
3. Для любых двух точек А и В существует такая точка С, что точка В лежит между А и С
4. Две прямые имеют не более одной общей точки
5. Из трех точек, лежаших на одной прямой, одна и только одна лежит между двумя другими
Вопрос 4. Найдите ошибку в определении интерпретации элементов модели Пуанкаре планиметрии Лобачевского.
1. Верхняя полуплоскость – это открытая полуплоскость, ограниченная горизонтальной прямой х
2. Абсолют - прямая х, граница верхней полуплоскости
3. Точки абсолюта – точки плоскости Лобачевского
4. Открытые полуокружности верхней полуплоскости с концами на абсолюте – неевклидовые прямые
5. Лучи полуплоскости с началом на абсолюте и перпендикулярные ему - также неевклидовые прямые
Вопрос 5. Найдите ошибку в описании элементов арифметической модели системы аксиом евклидовой планиметрии.
1. Любая упорядоченная пара целых чисел (х,у) - "точка", а число х,у- координаты "точки"
2. Уравнение ах 4- by + с = 0, где a, b Є R , а2 + b2 > 0 – «прямая»
3. Ось ординат - "прямая" х = 0
4. Ось абсцисс - "прямая" у = 0
5. Начало координат - "точка" (0,0)
Задание 6
Изучить материалы п. 1.1. части 1 части 3. Выписать определение первообразной от данной функции, формулировку теоремы существования первообразной (теорема 1). Составить конспект с доказательством теоремы 2 и леммы. Выписать определение неопределенного интеграла и формулировки его свойств. Составить таблицу основных интегралов и законспектировать общие правила интегрирования (А и В) с доказательствами.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Как называется функция, производная которой равна данной функции?
1. Неявная функции
2. Подинтегральная функция
3. Неопределенный интеграл
4. Первообразная функция
5. Дифференциальное выражение
Вопрос 2. Найдите ошибочное выражение, если F(x)- одна из первообразных для функции f(x), а С - произвольное постоянное.
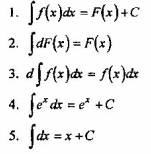
Вопрос 3. Какое из выражения является интегралом ![]()
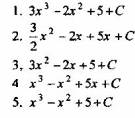
Вопрос 4. Какое из выражений является интегралом ![]()
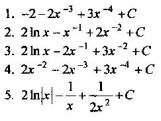
Вопрос 5. Какое из выражений является интегралом ![]()
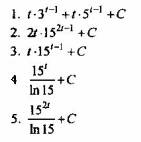
Задание 7
Изучить материалы п. 1.2. части 1 части 3. Законспектировать указания по применению методов замены переменной и интегрирования по частям. Разобрать примеры. Выписать отдельно формулы замены переменной и интегрирования по частям.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какую из подстановок целесообразно использовать для замены переменной в интеграле ![]()
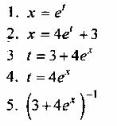
Вопрос 2. Какую из подстановок целесообразно использовать для замены переменной в интеграле 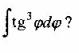
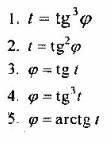
Вопрос 3. Какое из выражений целесообразно принять за и при интегрировании по частям интеграла 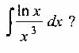
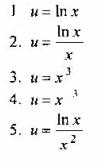
Вопрос 4. Какое из выражений целесообразно принять за и при интегрировании по частям интеграла ![]()
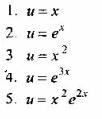
Вопрос 5. Какое из выражений является интегралом ![]()
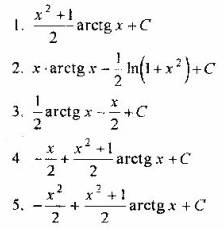
Задание 8
Изучить и законспектировать материалы п. 1.3. масти 1 части 3. Разобрать примеры. Выписать отдельно простейшие дроби всех четырех типов в общем виде.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из уравнений является разложением многочлена (х3 + 4х2 + 4х) на простейшие действительные множители?
1. х(х2 + 4х + 4)
2. (х (х + 4) + 4) х
3. х (х2+ 4 (х + 1))
4. х(х+2)2
5. х (х + 2)(х + 4)
Вопрос 2. Какой из многочленов имеет следующие действительные корни:
простой корень, равный 1;
корень второй кратности, равный (-2);
два сопряженных комплексных корня: i и (-i)?
1. (x + 1)(x - 2)2(x + i)(x - i)
2. (x + 1)(x2 – 4)(x2 + l)
3. (x – 1)(x + 2)2(x2 + l)
4. (х2 + х – 2)(х2 + l)
5. (x - l)(x + 2)2(x – i)2
Вопрос 3. Какая из рациональных дробей является неправильной?
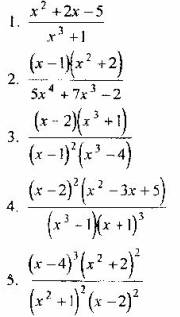
Вопрос 4. Какое ю выражений является представлением неправильной рациональной дроби 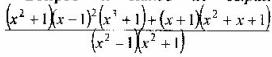 многочлена и правильной рациональной дроби?
многочлена и правильной рациональной дроби?
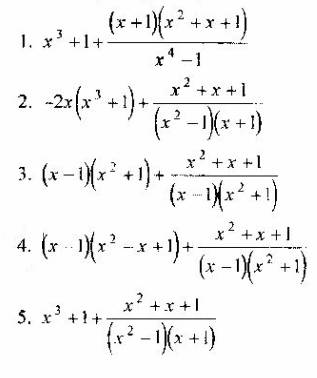
Вопрос 5. Какое из выражений является разложением рациональной дроби 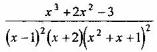 простейшие, где через А1, A2, B1, В2, М1, М2, N1, N2 обозначены неизвестные действительные числа.
простейшие, где через А1, A2, B1, В2, М1, М2, N1, N2 обозначены неизвестные действительные числа.
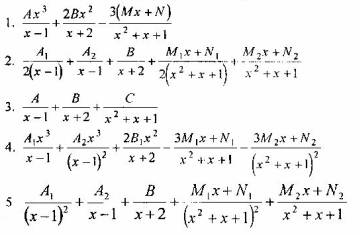
Задание 9
Изучить и законспектировать п. 1.4. части 1 раздела 3.
Разобрать примеры. Повторить материалы п. 1.3. в части методов решения простейших дробей III и IV типов. Повторить из курса алгебры методы решения систем линейных уравнений. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из выражений является разложением рациональной дроби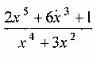 на целую часть и простейшие дроби
на целую часть и простейшие дроби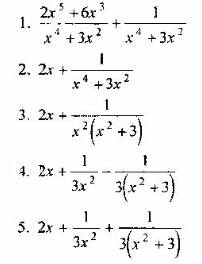
Вопрос 2. Найдите интеграл 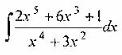
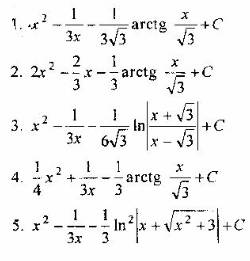
Вопрос 3. Какая подстановка позволяет найти интеграл 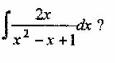
1. х – 1 = t
2. x – ¼ = t
3. x – ½ = t
4. x+1 = t
5. x + ½ =t
Вопрос 4. Найти интеграл 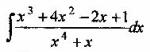
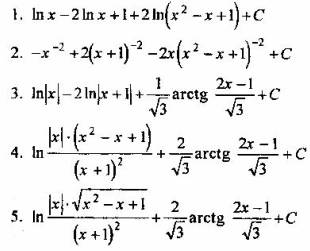
Вопрос 5. Какое выражение является иррациональным относительно функций ![]()
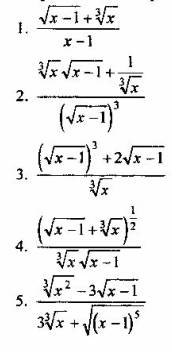
Задание 10
Изучить и законспектировать материалы п. 1.5. части 1 раздела 3. Разобрать примеры. Повторить основные формулы тригонометрии по школьному курсу алгебры. Выписать их отдельно. Так же выписать и законспектировать таблицу основных интегралов.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какой из примеров используется при интегрировании четной степени синуса или косинуса?
1. Понижение подинтегральной функции (вдвое) заменой sin2 х (cos2 x) по тригонометрическим формулам.
2. Отделение одного из множителей sinx (cosx) и замены его новой переменной.
3. Замена tgx или ctgx новой переменной.
4. Разложение на слагаемые по формулам произведения тригонометрических функций.
5. Интегрирование по частям.
Вопрос 2. Какой интеграл не выражается в элементарных функциях?
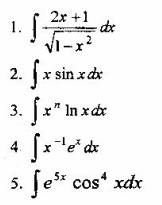
Вопрос 3. Найти интеграл ![]()
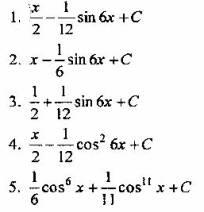
Вопрос 4. Найти интеграл ![]()
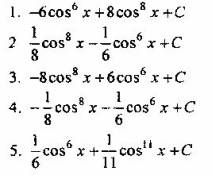
Вопрос 5. Найти интеграл 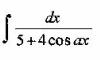
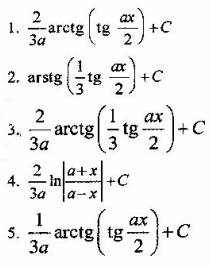
Задание 11
Изучить п. 2.1. части 2 раздела 3. Выписать определение и формулировку теоремы. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Чему равна площадь фигуры на рисунке?
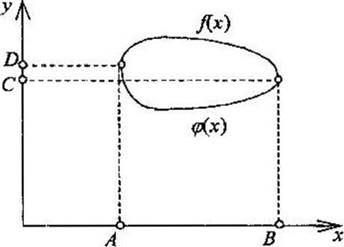
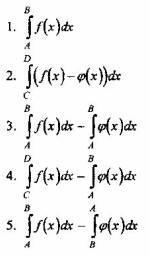
Вопрос 2. Если задана функция скорости v = f(t) при движении тела от точки А до точки В, что можно узнать интегрированием этой функции по времени?
1. Время движения тела от точки А до точки В
2. Скорость в точке В
3. Ускорение
4. Путь пройденный телом при движении от точки А до точки В
5. Расстояние между точками А и В
Вопрос 3. По какой переменной нужно проинтегрировать функцию силы, чтобы получить работу, совершенную при перемещении тела из точки А в точку В?
1. По пути
2. По времени
3. По скорости
4. По силе
5. По работе
Вопрос 4. Чему равна площадь заштрихованной фигуры?
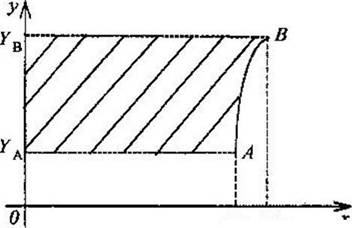
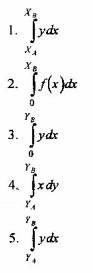
Вопрос 5. Какое из утверждений верно? Интеграл 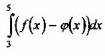 - это:
- это:
1. Функция от х
2. Функция от f(х)
3. Функция от f(х) и φ(х)
4. Функция от у = f(х) - φ(х)
5. Число
Задание 12
Изучить п. 2.2. части 2 раздела 3. Выписать формулировки теорем и законспектировать доказательства. Выучить определения.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Каков геометрический смысл определенного интеграла от функции у = f{x) в интервале [а, b] в системе декартовых координат?
1. Длина линии у = f(х) в интервале [а,b]
2. Алгебраическая площадь фигуры, ограниченной линией у = f(х) в интервале [a, b]
3. Среднее значение функции f(х) в интервале [а, b]
4. Произведение среднего значения функции в интервале [а, b] на длину интервала
5. Максимальное значение функции f(x) в интервале [a, b]
Вопрос 2. Чему равен интеграл 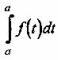 для любой непрерывной функции f(x):
для любой непрерывной функции f(x):
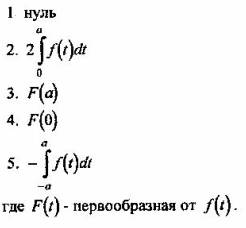
Вопрос 3. Чему равен интеграл 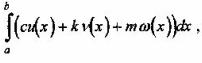 где с, к, т - константы:
где с, к, т - константы:
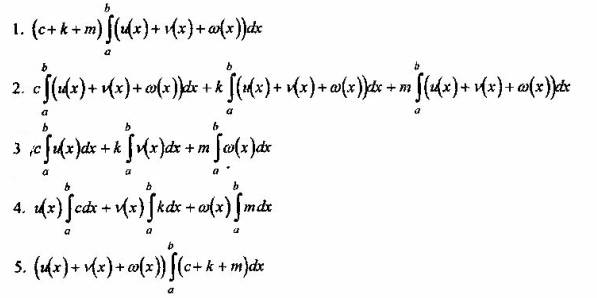
Вопрос 4. Какое из утверждений верно для любой непрерывной функции f(x)?

5. He вычисляя интеграл 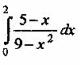 оценить границы его возможного значения, используя теорему об оценке определенного интеграла.
оценить границы его возможного значения, используя теорему об оценке определенного интеграла.
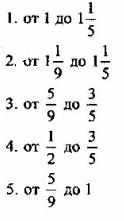
Задание 13
Изучить п. 2.3. части 2 раздела 3. Выписать формулировки теорем и их доказательства. Выучить определения. Обратить внимание на правила интегрировании по частям и замены переменных в определенном интеграле.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из следующих утверждений верно для любой непрерывной функции f(x), если F(х)- первообразная от f(х).
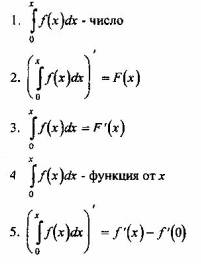
Вопрос 2. Вычислить интеграл, используя формулу интегрирования по частям 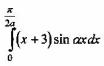 и выберите правильный ответ
и выберите правильный ответ
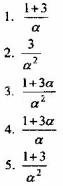
Вопрос 3. Вычислить интеграл, используя правило замены переменных 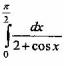
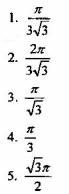
Вопрос 4. Не производя вычислений, укажите интеграл, равный нулю.
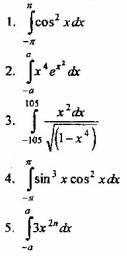
Вопрос 5. Вычислить интеграл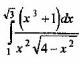
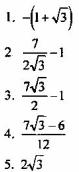
Задание 14
Изучить п. 2.4. части 2 раздела 3. Выучить определение, разобрать примеры. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какой из приведенных ниже интегралов является несобственным, если функция f(x) -непрерывна?
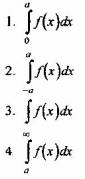
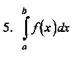
Вопрос 2. Чему равен интеграл ![]()
1. 1/8
2. Интеграл расходится
3.0
4. 2
5. 1/4
Вопрос 3. Чему равен интеграл 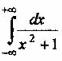
1. π/2
3. ∞
4. π
5. 2π
Вопрос 4. Какое из дифференциальных выражений является полным дифференциалом?
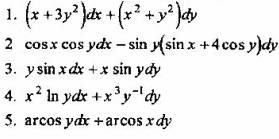
Вопрос 5. Какая из функций является первообразной для дифференциального выражения
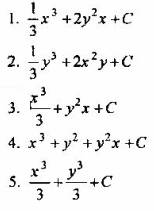
Задание 15
Изучить п. 1 части 4. Законспектировать.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из уравнений не является дифференциальным? (у функция от x).
1. у' = f(x)
2. f '(x) = С
3. у' + уеx = tg3x
4. dy = x
5. 2уу' = 1
Вопрос 2. Сколько частных решений имеет уравнение ху' = у + х?
2. 2
3. 7
4. 51
5. Бесконечное множество.
Вопрос 3. Сколько общих решений имеет дифференциальное уравнение ху' = у?
1. 1
2. 2
3. 100
4. 72
5. Бесконечное множество.
Вопрос 4. Что является условием наличия единственного частного решения уравнения у' = f(x,y) при условии y|x=x0 = у0?
1. Непрерывность функции f(x,y)
2. Интегрируемость функции f(x,у)
3. Непрерывность f(x,y) в области, содержащей точку (x0, y0)
4. Непрерывность функции f(x, у) и ее частной производной df / dx в некоторой области, содержащей точку (x0, y0)
5. Непрерывность функции f(x,y) и ее частной производной в некоторой области, содержащей точку
Вопрос 5. Какое из уравнений не является дифференциальным уравнением с разделяющимися переменными?
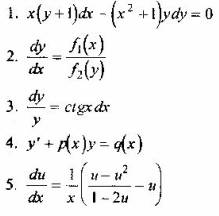
Задание 16
Изучить п. п. 1.3, 1.4 части 4. Законспектировать.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какой величине пропорциональна скорость радиоактивного распада?
1. Массе распавшегося вещества
2.Общей массе радиоактивного вещества
3. Массе нераспавшегося вещества
4. Температуре радиоактивного вещества
5. Произведению температуры и массы вещества.
Вопрос 2. Какое из дифференциальных уравнений нельзя свести к линейному?
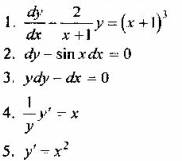
Вопрос 3. Какое из дифференциальных уравнений не является однородным?
1. (xy - y2)dx – (х2 - 2x)dy = 0
2. у' = (xy – y2) / (x2 – 2xy)
3. ху' = у
4. xy' = у +1
5. y’ = (x2)/ (y2)
Вопрос 4. К какому дифференциальному уравнению приводит задача о вытекании жидкости из цилиндрического сосуда через отверстие?
1. К нелинейному
2. К уравнению с разделяющимися переменными
3. К однородному
4. К дифференциальному уравнению второго порядка
5. К дифференциальному уравнению третьего порядка
Вопрос 5. Какое из дифференциальных уравнений описывает охлаждение тела в среде с постоянной температурой?
1. у' – C1(C2 - у), где С2 - температура среды, С1 - постоянная величина
2. (d2T) / (d2t) = -k(T -Тс), где Тс - температура среды, k - постоянная величина
3. dT = -к(T2 - Tc) dt, где Тс - температура среды, к - постоянная величина
4. dT =Tdt+T
5. dT = -kdt + kT , где к - постоянная величина
Задание 17
Изучить п.п. 1.1,5,1.4,2.1 части 4. Законспектировать.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из уравнений является уравнением в полных дифференциалах? (Установить с помощью проверки выполнения условия(dP/dy)/(dQ/dx))
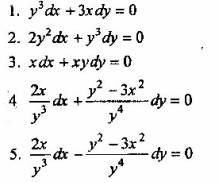
Вопрос 2. Как выглядит уравнение изоклины для уравнения у' = f(x, у)?
1. С=f(х,у)
2. f(x,y) = φ(y,z)
3. (dx/dy) = f(x,y)
4. х-у= 0
4. xdx + ydy = 0
Вопрос 3. Пусть с помощью графического метода Эйлера построена интегральная кривая у = φ(x) уравнения у' = f(х, у), причем при ее построении интервал [х0, х] разбивали на п частей точками х1, х2,..., хn-1. Какому условию удовлетворяет φ(х) ?
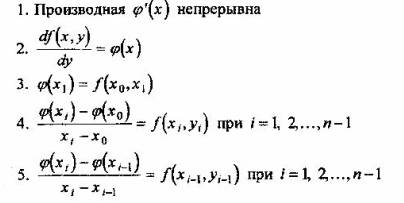
Вопрос 4. Какой вид имеет дифференциальное уравнение второго порядка?
1. y2= f(x,y, y’)
2. F(х, у, у’, у") = 0
3. F(х2, х, у2, у, у') = 0
4. (ay')2 + by' + су + dx = 0
5. f(x, y, y') = 0
Вопрос 5. Какой вид имеет общее решение дифференциального уравнения второго порядка?
1. у = φ(х,С1, С2, С3), где C1,С2,С3 - произвольные константы
2. y =φ(x,C1, C2), где С1, С2 - произвольные постоянные
3. y=φ(х)
4. у = φ(x,z)
5. у' = φ(х,С1,С2), где C1,C2 - произвольные постоянные
Задание 18
Повторить п. 2.1, изучить и законспектировать п.п. 2.2,2.3,2.4 части 4. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Сколько начальных условий необходимо задать для определения постоянных величин C1C2 в общем решении дифференциального уравнения второго порядка?
1. 1
2. 2
3. 3
4.4
5. 0
Вопрос 2. При каком условии можно утверждать, что существует решение уравнения у" = f(x,у,у'), удовлетворяющее условиям у|х=х0 = у0, y'|x=x0 = y’0
1. f(x,y,y') определена в точке (х0,у0,у'0)
2. f(x,y,y') = 0 в точке (х0,у0,y’0)
3. f(x,y, у') интегрируема в некоторой окрестности точки (х0, у0, у’0)
4. f(x,y,y’) непрерывна в точке (x0, y0, y’0)
5. f(x,y,y'0) непрерывна по у
Вопрос 3. К какому дифференциальному уравнению при решении сводится уравнение уу" + (у')2 = 0?
1. К уравнению в полных дифференциалах
2. К уравнению с разделяющимися переменными
3. К дифференциальному уравнению третьего порядка
4. К линейному дифференциальному уравнению первого порядка
5. К дифференциальному уравнению, не содержащему у
Вопрос 4. Чем определяется порядок дифференциального уравнения?
1. Количеством операций (шагов) при его решении
2. Количеством переменных величин в правой части
3. Максимальной степенью переменной х
4. Дифференцируемостью правой части уравнения
5. Высшим порядком производной, входящей в уравнение
Вопрос 5. Сколько произвольных постоянных величин содержит решение дифференциального уравнения 4-го порядка, если начальные условия не заданы?
1. 1
2. 2
3. 3
4.4
5. 5
Задание19
Изучить и законспектировать п.п. 3.1,3.2 части 4.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Какое из уравнений не сводится к линейному дифференциальному уравнению второго порядка?
1. 5у" - у' - 2у = lnx + 3у
2. у" + ху' +у = х
3. у" + у' =ху
4. y2+ y' + y = f{x)
5. (y’’ + y’) / (y) = f(x)
Вопрос 2. Под каким номером записано выражение, которое не может быть общим решением уравнения вида у" + a1y + а2у = 0 ни при каких значениях а1, а2?
1. C1e2x + C2е-х
2. С1е2x + С2хе2х
3. e3x (С1 cos4x + sin 4х)
4. С1е6х sin(x/2) - C2e6x cos(x/2)
5. ex(Clx - C2)
Вопрос 3. Под какими номером записано частное решение уравнения у" - 2у' – у = 0 при начальных условиях y|x=1 = 0, y’|x=1 = 0?
1. е2x
2. xex
3. cos2x
4. sin2x
5. 0
Вопрос 4. Под каким номером записано общее решение уравнения у" - 4 у' + 4у = 0 ?
1. С1е2х + С2
2. хС1 + С2е2x
3. (С1 +С2х)еx
4. C1e2x - C2xe2x
5. (С1ех +С2х)еx
Вопрос 5. Под каким номером записано общее решение уравнения у" + 25 у = 0?
1. еx(С1 cos5x + С2 sin5x)
2. C1e5x +С2
3. e5x (С1 + С2sin 5x)
4. С1 sin(5x + С2)
5. С1cosx + С2 sinx
Задание 20
Изучить и законспектировать п.п. 3.3,3.4 части 4.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Под каким номером записано общее решение уравнения у" + 6у' + 9у = 3 cos2x + 3 sin2х?
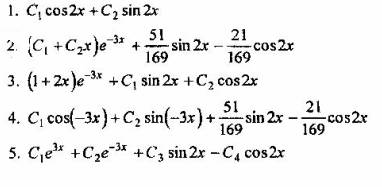
Вопрос 2. Какова степень многочлена Q(x) в частном решении у = Q(x)e5x уравнения у" -6у' + 9у = (х3 + 5х2 + 9)e5x ?
2. 2
3. 3
4.4
5. 5
Вопрос 3. Под каким номером указан вид частного решения уравнения у’’ + 9у = Р1 (x)cos 3х + Р2(x)sin 3x, где Р1(x),Р2(х) -многочлены четвертой степени?
1. у = е3х (R1(х) cos 3х + R2(x)sin 3х), где R1(х), R2(х) - многочлены третьей степени
2. у = е3х (R1(x)cos3x + R2(x)sin 3х), где R1(х), R2(х) - многочлены четвертой степени
3. y = x(R1(x)cos3х + R2(x)sin3х), где R1(x), R2(x) - многочлены четвертой степени
4. у = ex(R1(x)cos3x + R2(x)sin3x), где R1(х), R2(х) - многочлены пятой степени
5. у = R1(х) cos 3х + R 2 (х) sin 3х, где R1 (х), R2 (х) - многочлены шестой степени
Вопрос 4. Какое из уравнений не может быть решено методом вариации произвольных постоянных?
1. 5у " + 7у'+11y= lnх
2. у" + 7у' - 11у = 5x(x2 – sin(x/2))
3. у"- 5у = sinx · cos2x
4. еxу" + 7еxу' = 3ctgex
5. Любое из перечисленных уравнений может быть решено методом вариации произвольных постоянных
Вопрос 5. Под каким номером указан вид общего решения уравнения у" - 10у' = х2?
1. С1еx + С2е10х + Р(х)ех, где С1, С2 - произвольные постоянные, Р(х) - полином второй степени
2. С1 sinx + С2 cosl0x + Р(х), где С1,С2 - произвольные постоянные, Р(х) - полином третьей степени
3. С1 +С2е10х + Р(х)- где С1,С2 - произвольные постоянные, Р(х) - полином второй степени
4. С1 +С2е10х + хP(х)- где С1,С2 - произвольные постоянные, Р(х) - полином второй степени
5. C1e10x +С2Р(х) - где С1С2 - произвольные постоянные, Р(х) - полином второй степени
Задание 21
Изучить п.п. 3.5,3.6,3.7 части 4. Законспектировать п.п. 3.5, З.б части 4, повторить свойства определителей. Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Под какой цифрой записана система линейно зависимых функций?
1. sinx, cosx
2. sinx, cosx, tgx
3. х2 +1, х4 х3
4. ex, e2x, xex
5. x, x2 + 1, (x + 1)2
Вопрос 2. Какой из определителей является определителем Вронского?
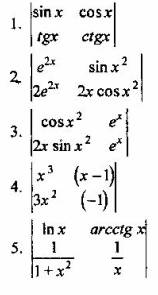
Вопрос 3. Предположим, что у1, у2, уз - фундаментальная система решений уравнения вида y’’’ - у"+ 2у' -3у = 0. Что можно сказать об определителе 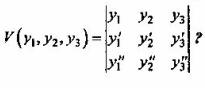

Вопрос 4. Предположим, что характеристическое уравнение r3 + а1r2 + а2r + a3 = 0 имеет корни: 1-2i, 1+2i, 5. Какова фундаментальная система решений соответствующего однородного дифференциального уравнения?
1.ex, e-2x, e5x
2. e5x ,хе2x, хе-2x
3. еx cos2x, xexcos2x, e5x
4. ех sin2х, хех sin2x, e5x
5. ех cos2x, ex sin 2х, е5х
Вопрос 5. Каким дифференциальным уравнением описываются свободные механические колебания?
1. Линейным дифференциальным уравнением первого порядка
2. Линейным однородным дифференциальным уравнением второго порядка
3. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами ненулевой правой частью I
4. Дифференциальным уравнением третьего порядка с ненулевой правой частью
5. Однородным дифференциальным уравнением третьего порядка
Задание 22
Изучить и законспектировать п.п. 3.7, 4.1 части 4.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. При каком условии ток в электрической цепи будет установившимся?
1. Если дифференциальное уравнение колебаний в электрической цепи является линейным однородным R fl
2.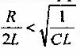 , где R – сопротивление, С – емкость, L – индуктивность электрической цепи
, где R – сопротивление, С – емкость, L – индуктивность электрической цепи
3. Правая часть уравнения 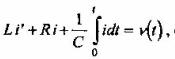 описывающего изменение тока в цепи не равна нулю
описывающего изменение тока в цепи не равна нулю
4. Правая часть уравнения ![]() описывающего изменение тока в цепи не равна нулю
описывающего изменение тока в цепи не равна нулю
5. Правая часть управления ![]() описывающего изменение тока в цепи равна нулю
описывающего изменение тока в цепи равна нулю
Вопрос 2. Сколько начальных условий определяют частное решение нормальной системы дифференциальных уравнений?
1. Столько же, сколько функций у1...уп составляют решение этой системы
2. В два раза больше, чем порядок дифференциальных уравнений в системе
3. Число начальных условий совпадает с порядком дифференциальных уравнений системы
4. Число начальных условий совпадает с максимальным числом переменных в правых частях дифференциальных уравнений системы
5. 2
Вопрос 3. Какая из систем дифференциальных уравнений не может быть приведена к нормальной?
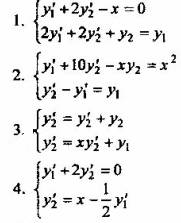
5. Все перечисленные системы приводятся к нормальным
Вопрос 4. Какое из дифференциальных уравнений не может быть сведено к нормальной системе дифференциальных уравнений?
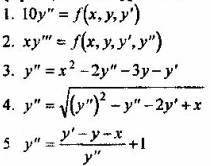
Вопрос 5. В каком случае задачу решения системы дифференциальных уравнений можно свести к задаче решения одного дифференциального уравнения, порядок которого равен числу уравнений системы?
1. Если правые части дифференциальных уравнений системы непрерывны вместе со своими частными производными при значениях х0, у10, у20,...,уn0
2. Если правые части дифференциальных уравнений системы линейно независимы
3. Если система уравнений является нормальной
4. Если число уравнений системы не превышает число начальных условий
5. Если система не может быть приведена к нормальной
Задание 23
Изучить и законспектировать п. 4.2 раздела 4.
Выбрать правильный ответ к вопросу и отметить его в карточке ответов.
Вопрос 1. Сколько систем частных решений образуют фундаментальную систему решений системы трех линейных однородных дифференциальных уравнений с постоянными коэффициентами?
3. 3
4. 4
5. Фундаментальную систему образует одно общее решение системы
Вопрос 2. При каком условии может быть получено частное решение системы линейных однородных дифференциальных уравнений с постоянными коэффициентами, удовлетворяющее любым заданным начальным условиям?
1. Наличие фундаментальной системы решений
2. Непрерывность функций, образующих некоторое частное решение
3. Интегрируемость функций, образующих общее решение
4. Определитель матрицы, строками которой являются частные решения системы дифференциальных уравнений при t = t0 не обращается в ноль
5. Определитель матрицы, строками которой являются частные решения системы дифференциальных уравнений равен нулю
Вопрос 3. Какой вид имеет частное решение системы линейных однородных дифференциальных уравнений с постоянными коэффициентами в случае действительных и различных корней характеристического уравнения k1,k2,…kn?
1. x1 = k1et, x2 = k2et, xn = knet,
2. x1 = sin k1t + cos k1t, x2 = sin k2t + cos k2t, …, xn = sin knt + cos knt
3. x1 = C1(sin k1t + cos k1t), x2 = С2 (sin k2t + cos k2t),..., xn = Cn (sin knt + cos knt), где C1, C2,...,Cn - постоянные величины
4. x1 = C1ek1t, x2 = C2ek2t, ... , xn = Cneknt, где C1,C2, … ,Cn - постоянные величины
5. Здесь нет частного решения
Вопрос 4. Какой вид имеет частное решение системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами в случае комплексных корней характеристического уравнения α + βi, α - βi?
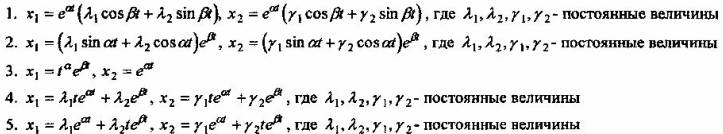
Вопрос 5. Под каким номером записано общее решение системы уравнений