Контрольная
Теория вероятности в СИБГАУ, вариант 1
550.00 руб
Дата сдачи: Май 2012
1. Используя диаграммы Вьенна, докажите тождество (A–B)+(B–A) = (A+B)–AB.
2. Зенитная батарея, состоящая из k орудий, производит залп по группе, состоящей из l самолетов (kбольше или равно l). Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, все k орудий выстрелят по одной и той же цели.
3. Происходит воздушный бой между двумя самолетами: истребителем и бомбардировщиком. Стрельбу начинает истребитель: он дает по бомбардировщику один выстрел и сбивает его с вероятностью p1. Если бомбардировщик этим выстрелом не сбит, он стреляет по истребителю и сбивает его с вероятностью p2. Если истребитель не сбит, он еще раз стреляет по бомбардировщику и сбивает его с вероятностью p3. Найти вероятность того, что будет сбит хотя бы один самолет.
4. Электрическая схема имеет вид:
Вероятности безотказной работы элементов А1, А2, А3 и А4 соответственно равны 0,9, 0,8, 0,9 и 0,7. Найти вероятность безотказной работы (т.е. не будет разрыва цепи), если элементы работают независимо друг от друга.
5. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможны в любой промежуток времени длительностью 3 сек. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше 0,8 сек. Найти вероятность того, что сигнализатор сработает за данное время, если каждое из устройств пошлет по одному сигналу.
6. Отдел маркетинга фирмы проводит опрос для выяснения мнений потребителей по определенному типу продуктов. Известно, что в местности, где проводятся исследования, 10% населения являются потребителями интересующего фирму продукта и могут дать ему квалифицированную оценку. Компания случайным образом отбирает 10 человек из всего населения. Чему равна вероятность того, что по крайней мере один человек из них может квалифицированно оценить продукт?
7. В первой урне содержится 5 зеленых и 4 голубых шаров, во второй – 3 зеленых и 6 голубых шаров. Из первой урны во вторую наудачу перекладывают 2 шара. После этого из второй урны наугад извлекают 3 шара. Найти вероятность того, что будут извлечены 2 голубых и 1 зеленый шар.
8. Вероятность одного попадания снаряда в цель равна 0,3. Сколько должно быть произведено независимых выстрелов, чтобы вероятность по меньшей мере одного попадания в цель была больше 0,9?
9. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. Если 3% счетов содержат ошибки, чему равна вероятность того, что аудитор найдет следующее: а) только один счет будет с ошибкой? 2) хотя бы один счет будет с ошибкой?
10. Посажено 600 семян кукурузы. Вероятность прорастания каждого семени равна 0,9. Найти вероятность того, что взойдет: а) ровно 550 семян; б) больше 535, но меньше 555 семян.
11. Менеджер ресторана по опыту знает, что 70% людей, сделавших заказ на вечер, придут в ресторан поужинать. В один из вечеров менеджер решил принять 20 заказов. Хотя в ресторане было лишь 15 свободных столиков. Чему равна вероятность того, что более 15 посетителей придут на заказанные места?
12. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле равна 1/4. Случайная величина – число израсходованных патронов. Найти закон распределения, построить многоугольник распределения, найти и изобразить функцию распределения, вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение данной случайной величины.
13. Процент людей, купивших новое средство от головной боли после того как увидели его рекламу по телевидению, есть случайная величина, заданная так:
5. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможны в любой промежуток времени длительностью 3 сек. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше 0,8 сек. Найти вероятность того, что сигнализатор сработает за данное время, если каждое из устройств пошлет по одному сигналу.
6. Отдел маркетинга фирмы проводит опрос для выяснения мнений потребителей по определенному типу продуктов. Известно, что в местности, где проводятся исследования, 10% населения являются потребителями интересующего фирму продукта и могут дать ему квалифицированную оценку. Компания случайным образом отбирает 10 человек из всего населения. Чему равна вероятность того, что по крайней мере один человек из них может квалифицированно оценить продукт?
7. В первой урне содержится 5 зеленых и 4 голубых шаров, во второй – 3 зеленых и 6 голубых шаров. Из первой урны во вторую наудачу перекладывают 2 шара. После этого из второй урны наугад извлекают 3 шара. Найти вероятность того, что будут извлечены 2 голубых и 1 зеленый шар.
8. Вероятность одного попадания снаряда в цель равна 0,3. Сколько должно быть произведено независимых выстрелов, чтобы вероятность по меньшей мере одного попадания в цель была больше 0,9?
9. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. Если 3% счетов содержат ошибки, чему равна вероятность того, что аудитор найдет следующее: а) только один счет будет с ошибкой? 2) хотя бы один счет будет с ошибкой?
10. Посажено 600 семян кукурузы. Вероятность прорастания каждого семени равна 0,9. Найти вероятность того, что взойдет: а) ровно 550 семян; б) больше 535, но меньше 555 семян.
11. Менеджер ресторана по опыту знает, что 70% людей, сделавших заказ на вечер, придут в ресторан поужинать. В один из вечеров менеджер решил принять 20 заказов. Хотя в ресторане было лишь 15 свободных столиков. Чему равна вероятность того, что более 15 посетителей придут на заказанные места?
12. Охотник, имеющий 4 патрона, стреляет в цель до первого попадания (или пока не израсходует все патроны). Вероятность попадания при каждом выстреле равна 1/4. Случайная величина – число израсходованных патронов. Найти закон распределения, построить многоугольник распределения, найти и изобразить функцию распределения, вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение данной случайной величины.
13. Процент людей, купивших новое средство от головной боли после того как увидели его рекламу по телевидению, есть случайная величина, заданная так:
|
xi |
0 |
10 |
20 |
30 |
40 |
50 |
|
pi |
0,10 |
0,20 |
0,35 |
0,20 |
0,10 |
0,05 |
а) Убедится, что задан ряд распределения. б) Найти функцию распределения. в) Определить вероятность того, что более 20% людей откликнуться на рекламу. г) Чему равен ожидаемый процент людей, откликнувшихся на рекламу? д) Чему равны дисперсия и среднее квадратичное отклонение?
14. Дискретная случайная величина X имеет только два возможных значения: x1 и x2, причем x1<x2. Вероятность того, что X примет значение x1 равно 0,7. Найти закон распределения X, зная математическое ожидание M[X] = –0,5 и дисперсию D[X] =5,25.
15. Функция распределения случайной величины X имеет вид
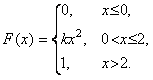
Найти: а) возможные значения параметра k, б) предполагая, что F(x) непрерывна в точке x=2, найти значение постоянной k, плотность f(x), D[4–2X] и квантиль х0,25
16. Масса товаров, помещаемых в контейнер определенного размера, – нормально распределенная случайная величина. Известно, что 65% контейнеров имеют чистую массу больше 4,9 т и 25% – имеют массу меньше, чем 4,2 т. найдите среднюю и среднее квадратичное отклонение чистой массы контейнера.
17. Артиллерия сделала 25 выстрелов по объекту. Вероятность попадания одного выстрела равно 0,2. Найти наивероятнейшее число попаданий, вероятность этого числа попаданий, математическое ожидание и дисперсию числа попаданий.
18. В наблюдениях Резерфорда и Гейгера радиоактивное вещество за промежуток времени 7,5 сек испускало в среднем 3,87 альфа-частиц. Найти вероятность того, что за 1 сек это вещество испустит хотя бы одну альфа-частицу.
19. Время безотказной работы прибора является случайной величиной, распределенной по показательному закону с параметром лямбда =0,002 ч–1. Найти математическое ожидание и дисперсию безотказной работы прибора, а также вероятность того, что прибор проработает 500 ч.
20. Найти распределение случайной величины Y, если Y=1/X, где случайная величина X имеет распределение Коши C(a,лямбда).
21. Даны законы распределения двух независимых дискретных случайных величин X и Y:
|
X |
0 |
1 |
2 |
|
Px |
0,5 |
0,3 |
0,2 |
|
Y |
0 |
3 |
|
Py |
0,4 |
0,6 |
Найти закон распределения случайной величины Z=XЧY и D[XЧY], а также коэффициент корреляции p[X,XY].
22. С помощью характеристической функции найти математическое ожидание M[X] и среднее квадратичное отклонение сигма [X] для геометрического распределения.

